CNN系列总结(一)---基础知识点

卷积操作的起源

卷积是微积分里的一个术语，指卷积运算。在图像处理中，卷积和滤波有很多应用，具体参考图像卷积与滤波的一些知识点。下图是卷积操作，Input是输入图片的像素矩阵，kernel是卷积核，选取一个滑动窗口，大小和卷积核一样，滑动窗口和卷积核进行点乘，得到的和作为输出像素值。CNN网络里的卷积核类似图像处理的卷积核(滤波器)，图像处理中的滤波器是事先定义好的，每个滤波器都有特定的功能(图像锐化、检测边缘等)。CNN网络利用神经网络的反向传播功能，通过损失函数来更新滤波器的值，使得滤波器能区分不同输入图像的共同点和不同点，对输入图片进行分类。

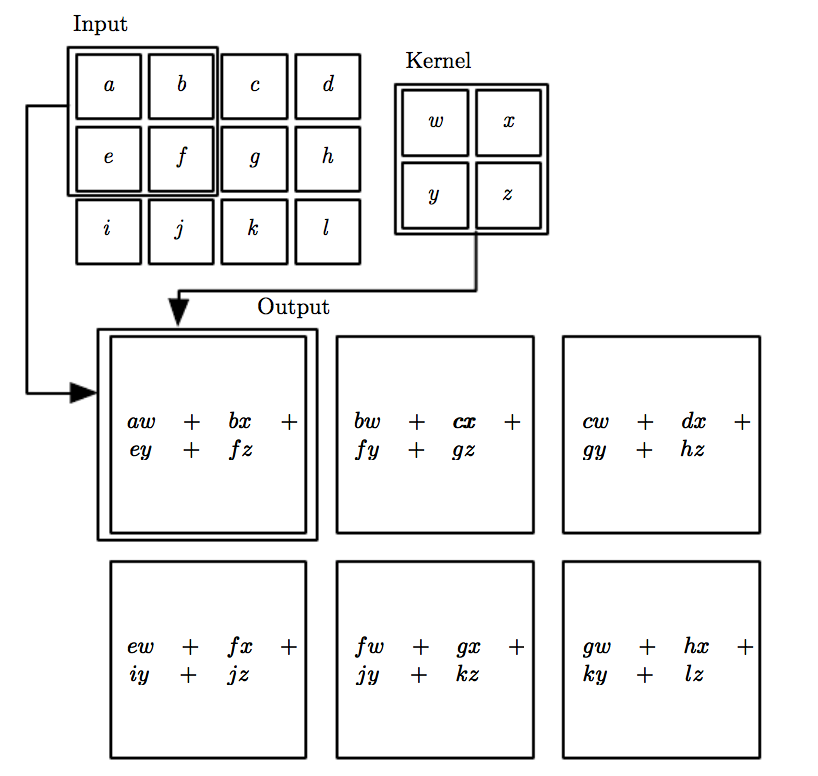
卷积层(Convolutional Layer)

举例来说，CNN网络在前向传播的时候，让每个滤波器(卷积核)都在输入数据的宽度和高度上滑动（更精确地说是卷积），然后计算整个滤波器和输入数据任一处的内积。当滤波器沿着输入数据的宽度和高度滑过后，滤波器与滑动窗口进行点乘，点乘结果经过激活函数(常用Relu)之后，会生成一个2维的激活图（activation map），激活图给出了在每个空间位置处滤波器的反应。网络会让滤波器学习到当它看到某些类型的视觉特征时就激活，具体的视觉特征可能是某些方位上的边界，或者在第一层上某些颜色的斑点，甚至可以是网络更高层上的蜂巢状或者车轮状图案。
卷积核直观上可以理解为具有学习功能的特征提取工具，提取目标物体的突出特征。

一般输入图像表示为(w x h x c)的矩阵，w和h表示输入图像的宽和高，c表示输入图像维度，如果是灰度图像，则c=1，如果是RGB图像，则c=3。在CNN网络里，输入图像一般有两种处理方式，一种是全转换为RGB图像，如果是灰度图像，则将二维矩阵(w x h)复制3次，变成(w x h x 3)；另一种是全转换为二维的灰度图像，像素值在0～255之间。

卷积层参数

步长(stride)：卷积核(滤波器)在输入数据上进行滑动时的间隔像素。如果滤波器的步长大于1，会使输出数据的尺寸小于输入数据。
零填充（zero-padding）：用0填充输入数据的边缘，0填充可以使输出数据和输入数据尺寸相同。
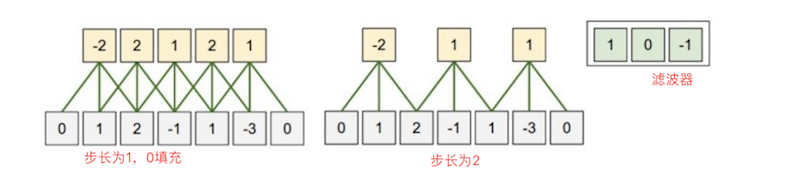
感受野（receptive field）：卷积核的空间尺寸，一般为3x3，5x5，7x7；感受野的尺寸(宽和高)是超参数，由用户自己定义，但是深度必须和输入数据的深度相等。注意：我们对待空间维度（宽和高）与深度维度是不同的：连接在空间（宽高）上是局部的，但是在深度上总是和输入数据的深度一致。
- 例1：假设输入数据体尺寸为[32x32x3]（比如CIFAR-10的RGB图像），如果感受野（或滤波器尺寸）是5x5，那么卷积层中的每个神经元会有输入数据体中[5x5x3]区域的权重，共5x5x3=75个权重（还要加一个偏差参数）。注意这个连接在深度维度上的大小必须为3，和输入数据体的深度一致。
- 例2：假设输入数据体的尺寸是[16x16x20]，感受野尺寸是3x3，那么卷积层中每个神经元和输入数据体就有3x3x20=180个连接。再次提示：在空间上连接是局部的（3x3），但是在深度上是和输入数据体一致的（20）。
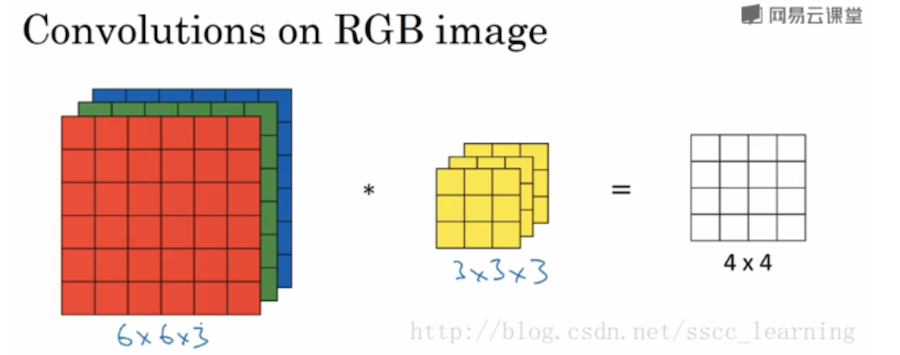
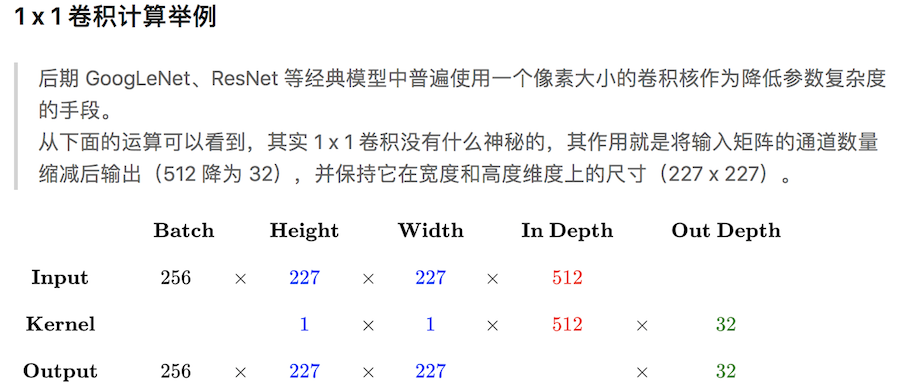
输出通道数(channel)：通道(channel)对输入数据是指数据的深度，比如RBG图像，channel是3；对输出数据是指卷积核的数量(不是深度，卷积核的深度与输入数据的深度保持一致)，如下图，有 6×6×3 的图片样本，使用 3x3 尺寸的卷积核（filter）进行卷积操作，那么输入图片的 channels 为 3，而卷积核的深度为3(与输入图片的深度保持一致)，所以卷积核是 3x3x3，如果只有1个卷积核，步长为1，不进行零填充。那么每一层卷积核中的27个数字与分别与每一层样本对应相乘后得到一个和，一共有3层，对这3层的卷积结果再进行求和，得到第一个结果。依次进行，最终得到 4×4的结果。如果卷积核个数为2，即 2x 3x3x3，那么结果为 2x4x4。

卷积层的计算细节

如图，输入图像IN是RGB图像，kernel大小是3x3x3，kernel数量(输出通道数)为5
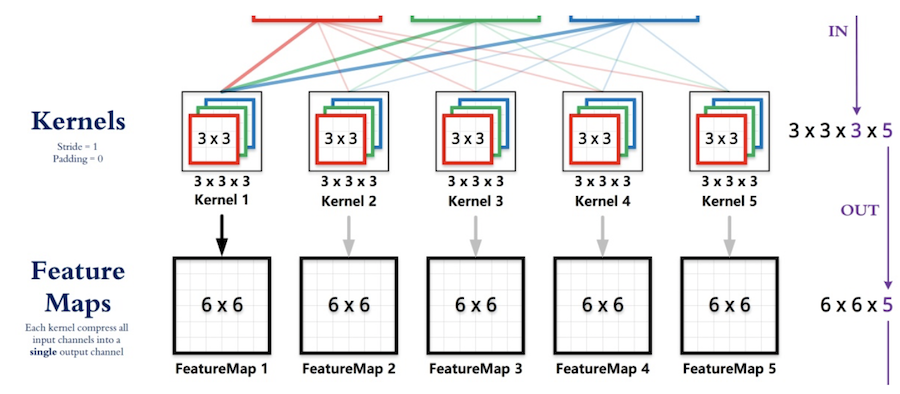
输入矩阵格式：四个维度，依次为：样本数、图像高度、图像宽度、图像通道数
输出矩阵格式：与输出矩阵的维度顺序和含义相同，但是后三个维度（图像高度、图像宽度、图像通道数）的尺寸发生变化。
权重矩阵（卷积核）格式：同样是四个维度，但维度的含义与上面两者都不同，为：卷积核高度、卷积核宽度、输入通道数、输出通道数（卷积核个数）
输入矩阵、权重矩阵、输出矩阵这三者之间的相互决定关系
- 卷积核的输入通道数（in depth）由输入矩阵的通道数所决定。（红色标注）
- 输出矩阵的通道数（out depth）由卷积核的输出通道数所决定。（绿色标注）
- 输出矩阵的高度和宽度（height, width）这两个维度的尺寸由输入矩阵、卷积核、扫描方式所共同决定。计算公式如下。（蓝色标注）

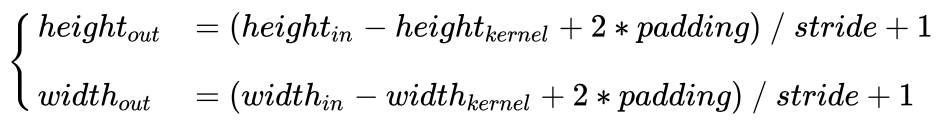
下图输入图像是RGB图像，大小是 7x7x3 (用0填充了一圈)，卷积核大小 3x3x3，用了2个卷积核，步长为2，输出结果为 3x3x2，下图在绿色的输出激活数据上循环演示，展示了其中每个元素都是先通过蓝色的输入数据和红色的滤波器逐元素相乘，然后求其总和，最后加上偏差得来。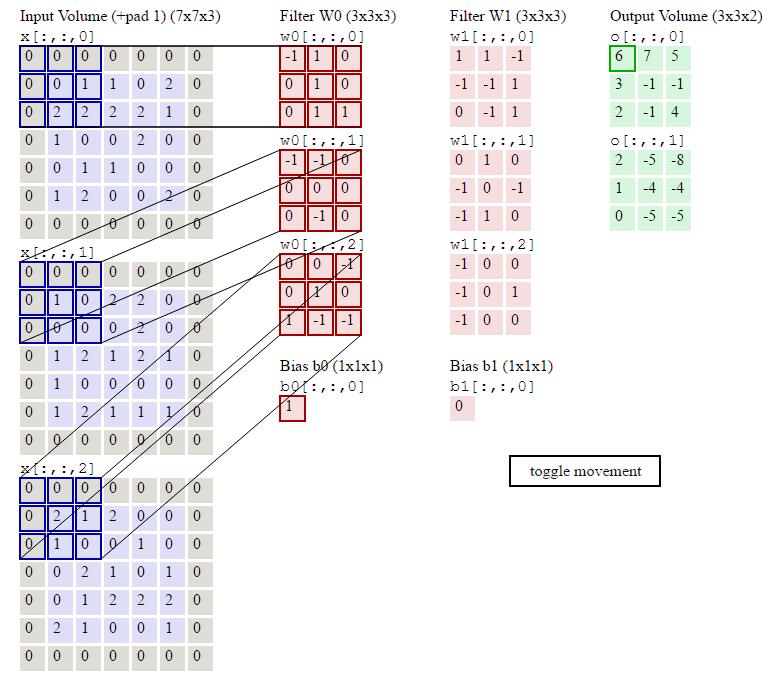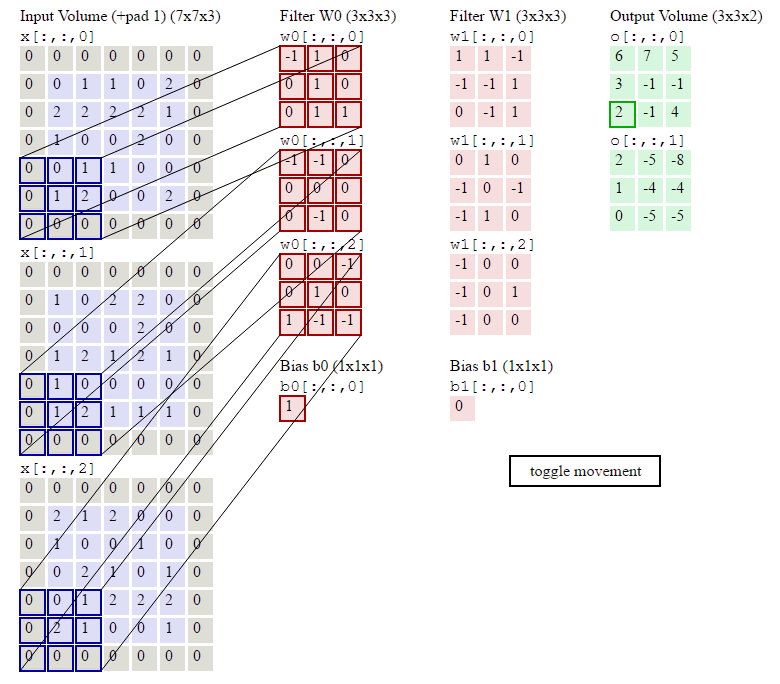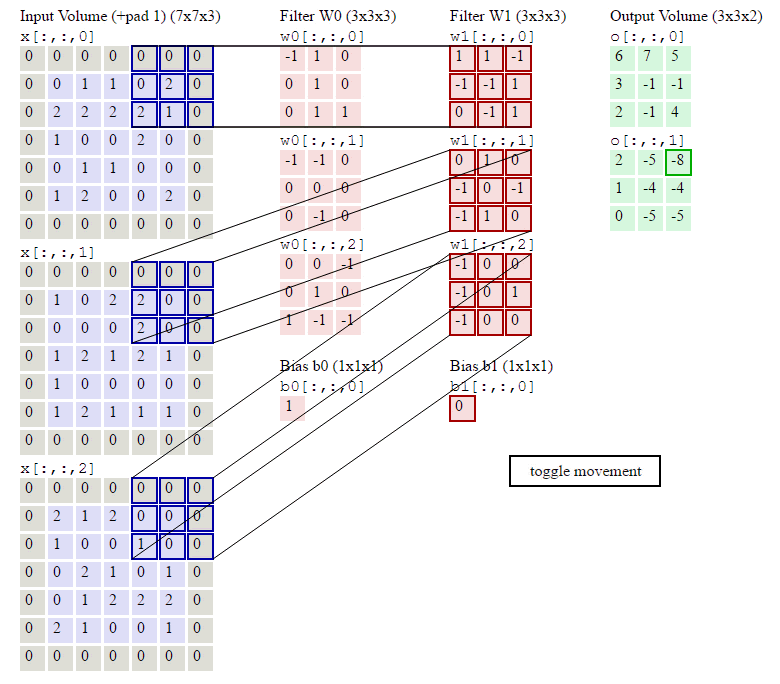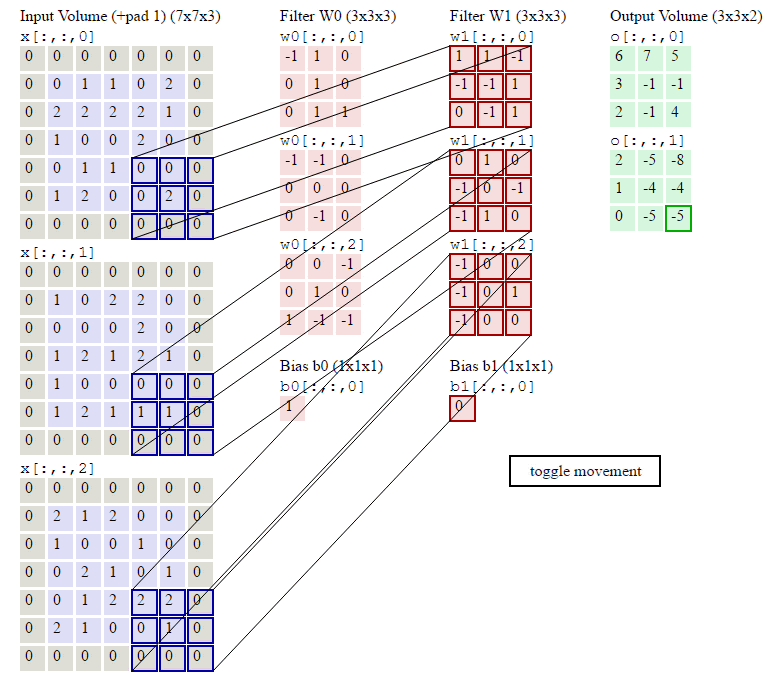

卷积层特点

1.大量的计算，网络的主要计算都产生在卷积层。
2.具有平移不变性，对待检测物体进行平移，不影响检测效果。
3.参数共享，控制参数的数量。
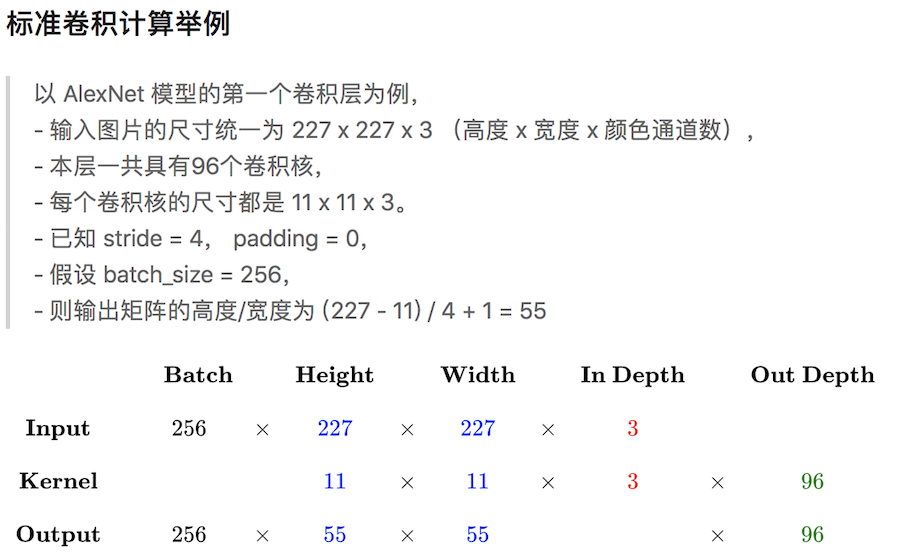
- Alex网络案例：Alex网络中输入图像的尺寸是[227x227x3]。在第一个卷积层，神经元使用的感受野尺寸F=11，步长S=4，不使用零填充P=0。因为(227-11)/4+1=55，卷积层的深度K=96，则卷积层的输出数据体尺寸为[55x55x96]。55x55x96个神经元中，每个都和输入数据体中一个尺寸为[11x11x3]的区域全连接。在深度列上的96个神经元都是与输入数据体中同一个[11x11x3]区域连接，但是权重不同。
- 参数计算：假设参数不共享，在第一个卷积层就有55x55x96=290,400个神经元，每个有11x11x3=364个参数和1个偏差。将这些合起来就是290400x364=105,705,600个参数。单单第一层就有这么多参数，显然这个数目是非常大的。
- 参数计算：假设参数共享， Alex网络案例中的第一个卷积层就只有96个不同的权重集了，一个权重集对应一个深度切片，共有96x11x11x3=34,848个不同的权重，或34,944个参数（+96个偏差）。在每个深度切片中的55x55个权重使用的都是同样的参数。在反向传播的时候，都要计算每个神经元对它的权重的梯度，但是需要把同一个深度切片上的所有神经元对权重的梯度累加，这样就得到了对共享权重的梯度。这样，每个切片只更新一个权重集。
  - 深度切片：将深度维度上一个单独的2维切片看做深度切片（depth slice），比如一个数据体尺寸为[55x55x96]的就有96个深度切片，每个尺寸为[55x55]。
- 参数共享的假设是有道理的：如果在图像某些地方探测到一个水平的边界是很重要的，那么在其他一些地方也会同样是有用的，因为图像结构具有平移不变性。
4.卷积操作通常后面接的是ReLU层，对激活图中的每个元素做激活函数运算。

反卷积(Deconvolution)

反卷积，它有这几个比较熟悉的名字，例如转置卷积、上采样、空洞卷积、微步卷积，但我们认为，最直接的就是反卷积=上采样=（转置卷积+微步卷积）⊆ 空洞卷积=一般意义上的广义卷积（包含上采样和下采样）。
如下图，输入feature map尺寸是 2x2，经过转置卷积后，尺寸是 4x4。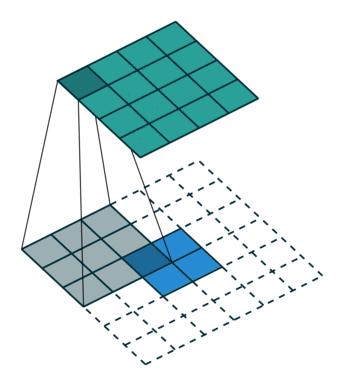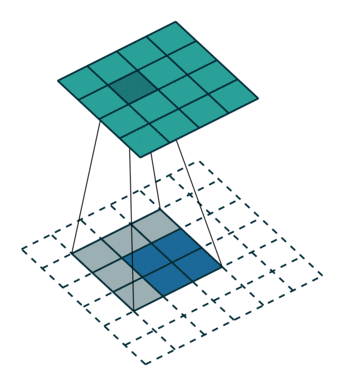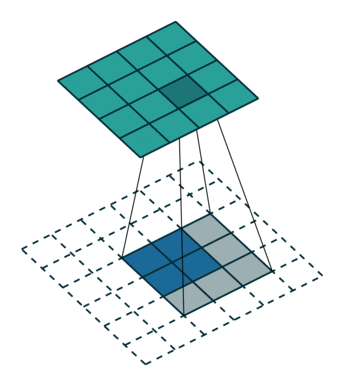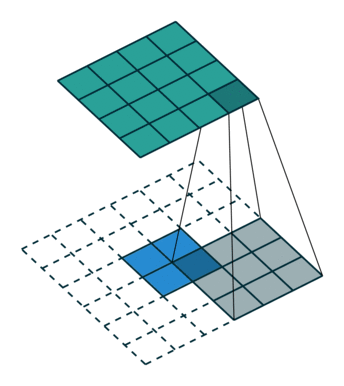

Deconvolution大致可以分为以下几个方面：

(1）unsupervised learning，其实就是covolutional sparse coding[1][2]：这里的deconv只是观念上和传统的conv反向，传统的conv是从图片生成feature map，而deconv是用unsupervised的方法找到一组kernel和feature map，让它们重建图片。
(2) CNN可视化[3]：通过deconv将CNN中conv得到的feature map还原到像素空间，以观察特定的feature map对哪些pattern的图片敏感，这里的deconv其实不是conv的可逆运算，只是conv的transpose，所以tensorflow里一般取名叫transpose_conv。
(3) upsampling[4][5]：在pixel-wise prediction比如image segmentation[4]以及image generation[5]中，由于需要做原始图片尺寸空间的预测，而卷积由于stride往往会降低图片size，所以往往需要通过upsampling的方法来还原到原始图片尺寸，deconv就充当了一个upsampling的角色。

[1] Zeiler M D, Krishnan D, Taylor G W, et
al. Deconvolutional networks[C]. Computer Vision and Pattern Recognition, 2010.
[2] Zeiler M D, Taylor G W, Fergus R, etal. Adaptive deconvolutional networks for mid and high level featurelearning[C]. International Conference on Computer Vision, 2011.
[3] Zeiler M D, Fergus R. Visualizing and
Understanding Convolutional Networks[C]. European Conference on Computer
Vision, 2013.
[4] Long J, Shelhamer E, Darrell T, et al.Fully convolutional networks for semantic segmentation[C]. Computer Vision andPattern Recognition, 2015.
[5] Unsupervised Representation Learning
with Deep Convolutional Generative Adversarial Networks

池化层(Pooling Layer)

Pooling Layer也叫汇聚层，通常每个卷积层之后会紧跟Relu，激活需要学习的特征，连续的卷积层(包含Relu)之后，会插入一个池化层，池化层的作用是降维，主要是降低输出数据的空间尺寸(不改变深度)，这样也能减少网络的参数量，也能有效控制过拟合。池化层一般用一个2x2的滤波器，步长为2进行卷积，常见的操作有对2x2(滤波器对应的输入数据块)的数据取最大值、取平均值等。
池化层在输入数据体的每个深度切片上，独立地对其进行空间上的降采样。下图中，左边：输入数据体尺寸[224x224x64]被降采样到了[112x112x64]，采取的滤波器尺寸是2，步长为2，而深度不变。右边：最常用的降采样操作是取最大值，也就是最大池化，这里步长为2，每个取最大值操作是从4个数字中选取（即2x2的方块区域中）。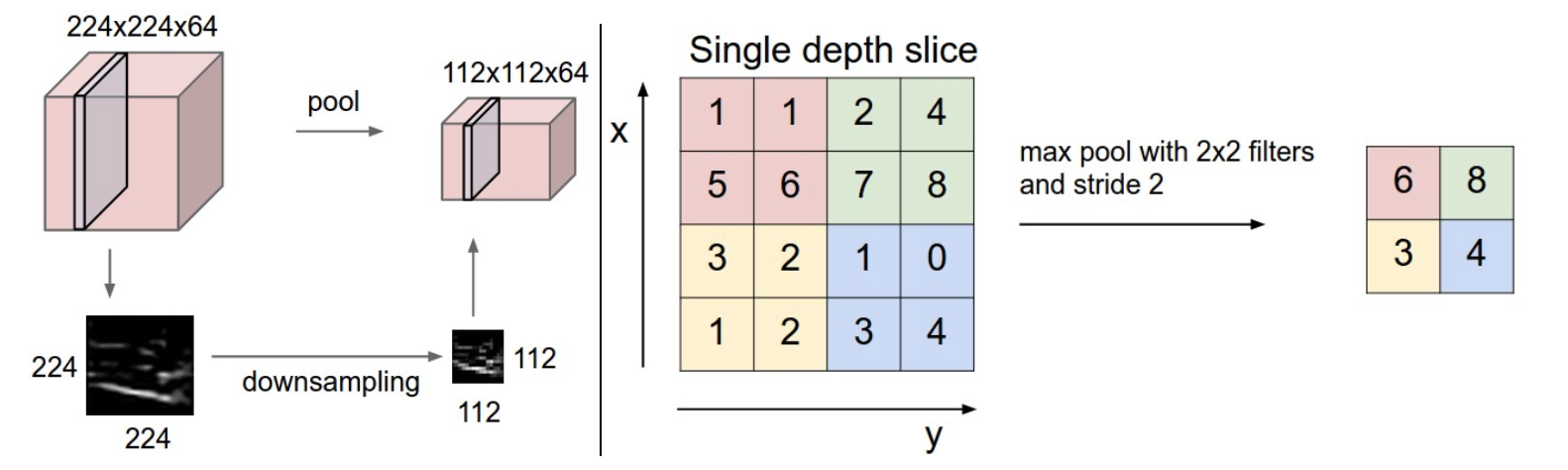

池化层的反向传播：max(x, y) 的反向传播可以简单理解为将梯度只沿最大的数回传，因此在向前传播经过池化层的时候，会把池中最大元素的索引记录下来，这样在反向传播的时候梯度的路由就很高效。
不使用池化层：池化层不是必须的，目前有一些方法可以替代池化层，比如卷积层中使用更大的步长来降低数据体的尺寸。

全连接层(Fully-Connected Layer)

全连接层和普通的神经网络一样。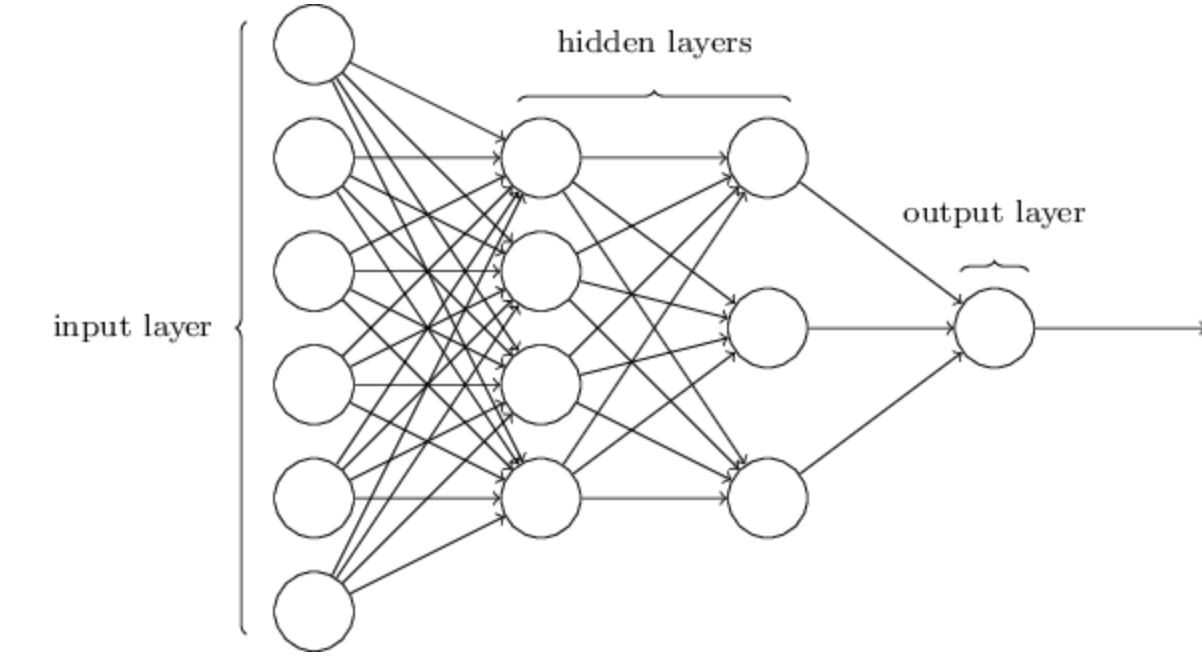

全连接层的作用是将卷积提取的特征映射到每一类，方便损失函数打分。全连接层的输入是前一层的所有神经元个数，输出是用户自定义，一般最后一层全连接层的输出个数是需要检测物体的类别数(对于分类网络)。

全连接层转化为卷积层

全连接层与卷积层的区别
- 1.卷积层的输入是输入矩阵的一块区域，全连接层的输入必须是一个列向量；
- 2.卷积层是局部连接，全连接网络使用了图像的全局信息；
  全连接层和卷积层的相同点都是神经元进行点积运算。
卷积层代替全连接层的好处：如果网络使用了全连接层，那么输入数据的尺寸一般是固定(因为全连接层的权重矩阵是固定的，所以最后输入全连接层的feature map的尺寸也是固定的)。但是如果用卷积层代替全连接层，就可以输入任意尺寸的数据了。
如何转化
- 最初是Jonathan Long发表的《Fully Convolutional Networks for Semantic Segmentation》论文，提出了FCN（全卷积网络），用于图像语义分割。
- 任何全连接层都可以被转化为卷积层。比如，一个 K=4096 的全连接层，输入数据体的尺寸是 7x7x512，这个全连接层可以被等效地看做一个卷积核尺寸 F=7, 零填充 P=0, 步长 S=1, 卷积核数量 K=4096的卷积层。换句话说，就是将滤波器的尺寸设置为和输入数据体的尺寸一致了。因为只有一个单独的深度列覆盖并滑过输入数据体，所以输出将变成 1x1x4096，这个结果就和使用初始的那个全连接层一样了。
- 举例说明，如果一幅图片经过卷积网络之后，feature map为7x7x4096，类别有10类，那么如果这里接full connection层它的参数数量为 7x7x4096x10，但是我们可以换一种思路，下一层用卷积层实现同样功能，那么就是需要10个7*7的filter，filter的深度为4096，这样我们会发现参数的数量相同，并且计算的时间复杂度以及空间复杂度等等都没有区别，那么为什么还要用卷积层呢？
  这主要是为了解决当图片中有多个类别物体的情况下，某一个物体最后映射的feature map是 7x7，但是这幅图中还有其他物体，这样最后我们不仅仅需要得到一个一维向量 1x1x10，事实上我们需要的假如说是 6x6x10，我们需要对 6x6 的每个网格都做分类，那么这时候如果用full connect层，需要经过多次全连接层，才能得到 6x6x10 个score feature，而如果用卷积层，就可以通过利用滑动窗口，一次前向传播就得到 6x6x10 的score feature，这样无疑是更加高效的，因为这样只需要计算每个位置卷积不同的地方即可，事实上不同的地方很小。

CNN网络的结构

CNN网络结构一般包含卷积层、池化层、全连接层、激活函数、反向传播。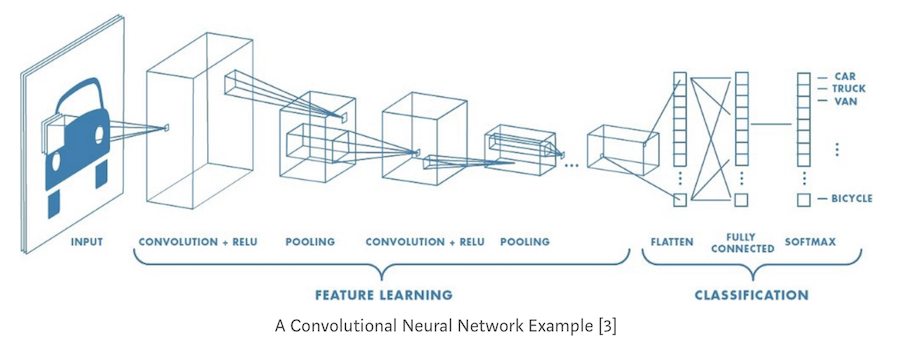

CNN网络最常见的形式就是将一些卷积层和ReLU层放在一起，其后紧跟池化层，然后重复如此直到图像在空间上被缩小到一个足够小的尺寸，在某个地方过渡成成全连接层也较为常见。最后的全连接层得到输出，比如分类评分等。换句话说，最常见的CNN网络结构如下：

1	INPUT -> [[CONV -> RELU]\N -> POOL?]\M -> [FC -> RELU]\*K -> FC

其中 * 指的是重复次数，POOL? 指的是一个可选的汇聚层。其中N >=0,通常N<=3,M>=0,K>=0,通常K<3。例如，下面是一些常见的网络结构规律：

INPUT -> FC,实现一个线性分类器，此处N = M = K = 0。
INPUT -> CONV -> RELU -> FC
INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC。此处在每个池化层之间有一个卷积层。
INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC。此处每个池化层前有两个卷积层，这个思路适用于更大更深的网络，因为在执行具有破坏性的池化操作前，多重的卷积层可以从输入数据中学习到更多的复杂特征。

几个小滤波器卷积层的组合比一个大滤波器卷积层好： 假设你一层一层地重叠了3个3x3的卷积层（层与层之间有非线性激活函数）。在这个排列下，第一个卷积层中的每个神经元都对输入数据体有一个3x3的视野。第二个卷积层上的神经元对第一个卷积层有一个3x3的视野，也就是对输入数据体有5x5的视野。同样，在第三个卷积层上的神经元对第二个卷积层有3x3的视野，也就是对输入数据体有7x7的视野。假设不采用这3个3x3的卷积层，二是使用一个单独的有7x7的感受野的卷积层，那么所有神经元的感受野也是7x7，但是就有一些缺点。首先，多个卷积层与非线性的激活层交替的结构，比单一卷积层的结构更能提取出深层的更好的特征。其次，假设所有的数据有C个通道，那么单独的7x7卷积层将会包含 Cx(7x7xC)=49C^2 个参数，而3个3x3的卷积层的组合仅有 3x(Cx(3x3xC))=27C^2 个参数。直观说来，最好选择带有小滤波器的卷积层组合，而不是用一个带有大的滤波器的卷积层。前者可以表达出输入数据中更多个强力特征，使用的参数也更少。唯一的不足是，在进行反向传播时，中间的卷积层可能会导致占用更多的内存。

CNN网络耗费的内存资源

在构建CNN网络结构时，最大的瓶颈是内存瓶颈。大部分现代GPU的内存是3/4/6GB，最好的GPU大约有12GB的内存。要注意三种内存占用来源：

来自中间数据体尺寸：卷积神经网络中的每一层中都有激活数据体的原始数值，以及损失函数对它们的梯度（和激活数据体尺寸一致）。通常，大部分激活数据都是在网络中靠前的层中（比如第一个卷积层）。在训练时，这些数据需要放在内存中，因为反向传播的时候还会用到。但是在测试时可以聪明点：让网络在测试运行时候每层都只存储当前的激活数据，然后丢弃前面层的激活数据，这样就能减少巨大的激活数据量。
来自参数尺寸：即整个网络的参数的数量，在反向传播时它们的梯度值，以及使用momentum、Adagrad或RMSProp等方法进行最优化时的每一步计算缓存。因此，存储参数向量的内存通常需要在参数向量的容量基础上乘以3或者更多。
各种零散的内存占用，比如成批的训练数据，扩充的数据等等。

一旦对于所有这些数值的数量有了一个大略估计（包含激活数据，梯度和各种杂项），数量应该转化为以GB为计量单位。把这个值乘以4，得到原始的字节数（因为每个浮点数占用4个字节，如果是双精度浮点数那就是占用8个字节），然后多次除以1024分别得到占用内存的KB，MB，最后是GB计量。如果你的网络工作得不好，一个常用的方法是降低批尺寸（batch size），因为绝大多数的内存都是被激活数据消耗掉了。

下一篇 CNN系列总结(二)—经典模型结构